Navigation orthodromique du grande cercle sur une orange


Si jamais vous avez le vol de Londres ou de Hambourg à Los Angeles, peut-être vous avez remarqué que, au début vous volez presque au nord-ouest, pour finalement arriver en Californie avec le cours sud-ouest. La distance la plus courte entre 2 endroits sur le globe ne suit pas un cours sûr boussole droite qui le capitaine pourrait suivre tout le chemin. Ce connaissait déjà les vieux marins, le cours sûr boussole doit être changé de façon permanente. Ceci est appelé navigation du grand cercle, puisque vous voyagez sur un parcours orthodromique dans le monde entier.
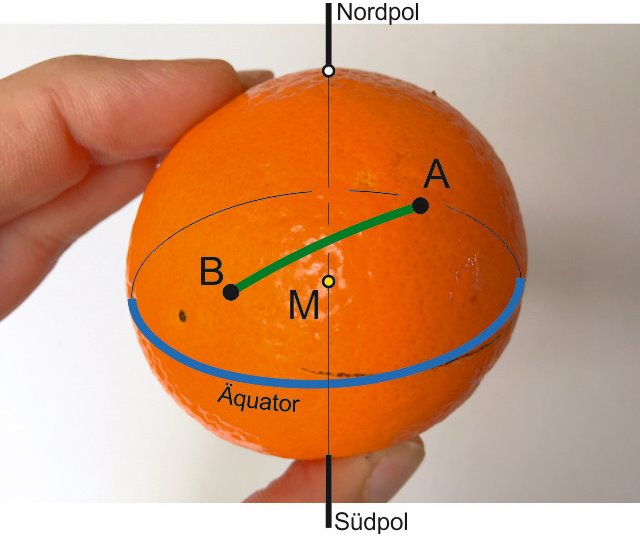
nous voulons naviguer de A à B, les coordonnées (longitude et latitude) de départ et de destination sont connus, ce que nous voulons savoir:
- la distance
- Le cours sûr boussole nous devons suivre
La distance peut être calculée par la relation suivante, tirée de sources pertinentes (Wikipedia)


Si nous convertissons maintenant le résultat de degrés à arcminutes (multiplié par 60), on obtient la distance entre A et B en miles nautiques (une minute d'arc sur un grand cercle correspond par définition à un mile nautique).
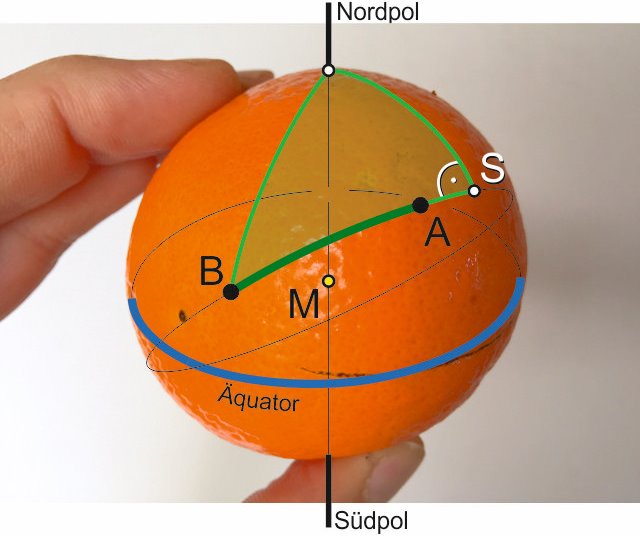
Jusqu'ici tout va bien. Maintenant, le cours. La navigation classique propose la méthode du "triangle de navigation" qui est un triangle sphérique rectangle, nommé "pôle-triangle" et forme un angle droit au sommet (S) entre le cours du grand cercle et la distance au pôle Nord (ou Pôle Sud):
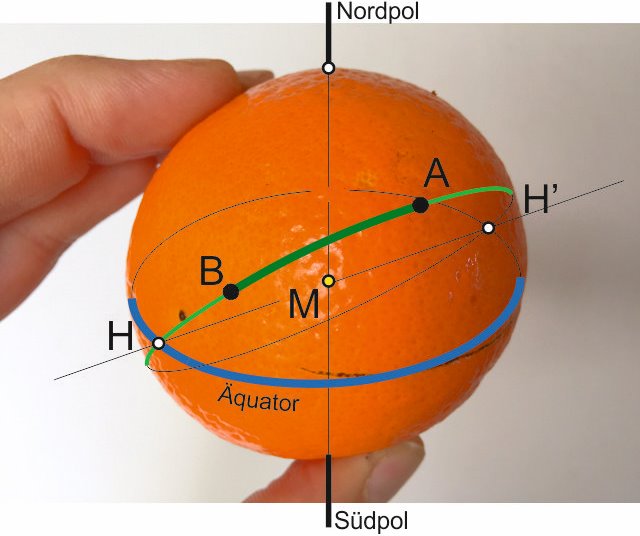
Après avoir été un temps occupé avec cela, je me souvins d'une méthode plus simple de comprendre pour moi. Comme un vieux penseur intransigeant, je préfère me orienter vers l'équateur plutôt qu'au pôle Nord (peut-être simplement parce qu'il est plus chaud là...) J'utilise ici le fait que chaque grand cercle recoupe exactement deux fois avec l'autre grand cercle sur le même monde, à savoir à 2 points exactement opposés de la sphère (appelons-les H). Il en va également de l'équateur avec notre cours grand cercle, comme suit:
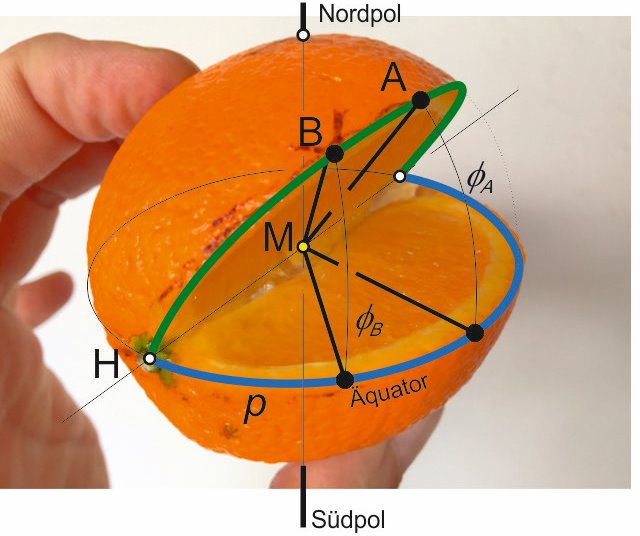
Pour le rendre un peu plus facile pour l'oeil humain, je coupe notre orange, coupé exactement sur la partie où l'équateur croise notre cours du grand cercle, le résultat est le suivant:
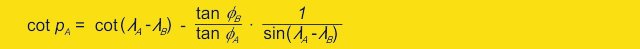
Je vais éviter d'expliquer la dérivation de cette équation pour le moment, les personnes intéressées peuvent trouver ci-dessous sur cette page.
pA nous dit les longitudes à passer pour avoir le baptême équatorial, ou parlé comme une fruiterie, au sommet de notre couper d'orange.
Et avec l'équation suivante, on obtient l'angle du couper d'orange:

(Dérivation pour les personnes intéressées à nouveau ci-dessous.)
Et maintenant, ce que nous voulions vraiment, une équation avec laquelle on peut déterminer la latitude correspondante sur le grand cercle pour toute longitud donnée:

(Dérivation comme toujours ci-dessous)
On pourrait encore continuer avec cela, par exemple, il serait très intéressant pour chaque point de référence, savoir le cours nous devrions naviguer (changer le cours sûr boussole), ou vous pourriez déterminer la longitude en fonction de la latitude, ou même une formule pour le cours en fonction de la distance déjà navigué. Avec les bases déjà développées, on peut tirer tout cela relativement rapidement avec trigonométrie sphérique, mais oui, je ne vais pas exagérer ici...
Ce que nous avons laissé est un
exemple de calcul:
Nous venons du Cap Horn, et nous tenons à traverser le Pacifique pour arriver sur les îles Fiji. Bien sûr, nous ne le ferions pas normalement, mais comme un exemple de calcul il fonctionne agréable :-)
Cap Horn:
55 degrés 59 min S = -55,98 degrés
67 degrés 17 min W = -67,28 degrees
îles Fiji:
18 degrés 8 min S = -18,13 degrés
178 degrés 26 min O = 178,43 degrés
Tout d'abord, nous déterminons la distance que nous devons naviguer:


= -0,8288 x -0,3112 + 0,5595 x 0,9504 x -0,4114
= -0,0400
arc cos -0,0400 = 87,71 degrees (x 60)
= 5.262 miles nautiques
Maintenant, nous définissons le pA nécessaire:
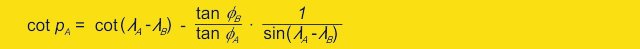
= -0,4513 - 0,2210 x 1,0971
= -0,6938
pA = -55,25 degrés
ainsi que l'angle du couper d'orange:

= -0,6750 x -0,8216
= 0,5545
l'angle du couper est donc 61 degrés.
pA est négatif: c'est seulement à cause que on n'a pas atteint le sommet de notre grand cercle lors de notre voyage, de sorte que cette valeur est réfléchie à l'intersection derrière nous (H' à la place de H), respectivement l'angle.
Maintenant, nous voulons déterminer cinq endroits sur le grand cercle, chacun au début et à la fin, et trois entre les deux. Notre formule:

Nos longitudes préétablies sont: -67,28 degrés (Cap Horn, début); 178,43 degrés (îles Fiji, fin); ainsi que -95 degrés; -125 degrés; -150 degrés. Donc, nous calculons aussi le départ et la destination, bien que les latitudes sont déjà connues, juste pour vérifier l'exactitude du calcul.
= 1,8034 x -0,8216 = -1,4817 -> latitude = -55,98 degrés, ok pour Cap Horn
= 1,8034 x -0,1815 = -0,3274 -> latitude = -18,13 degrés, ok pour îles Fiji
et les 3 points de référence:
= 1,8034 x -0,9925 = -1,7899 -> latitude = -60,81 degrés
= 1,8034 x -0,9207 = -1,6604 -> latitude = -58,94 degrés
= 1,8034 x -0,6695 = -1,2074 -> latitude = -50,36 degrés
Notre cours du grand cercle nous emmène donc du Cap Horn au départ vers le sud à 61 degrés de latitude (= l'angle du couper d'orange), probablement nous devons nous battre dur avec de la glace là avant, que nous nous dirigerons vers le nord et il va se réchauffer vers l'équateur...
John Franklin, Amerigo Vespucci et Sir Francis Drake vous saluer, que vous n'oubliez pas votre sextant sur le voyage s'il vous plaît, parce qu'ils étaient tous de grands mathématiciens et étaient voile encore sans GPS...
"Il y a quelque chose plus important que la logique: l'Imagination", Alfred Hitchcock
Derivations:
Nous considérons le triangle sphérique entre l'équateur, notre cours de grand cercle, et un point arbitraire P (voir l'image 5 ci-dessous). Ce triangle a d'excellentes propriétés, il est en fait un triangle sphérique à angle droit et permet donc des calculs facilement. Nous sommes intéressés par l'emplacement exact du couper d'orange, où notre parcours traverse l'équateur, et l'angle sous lequel on coupe l'orange. Connu sont 2 places P, le départ et la destination, chacune avec la latitude et la longitude. Dans ce triangle, nous utilisons un théorème de trigonométrie sphérique:

maintenant nous remplaçons hA, hB et Dp avec notre nomenclature précédente:
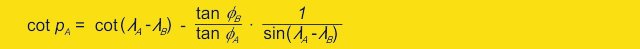
à partir de l'équation initiale, on obtient aussi l'angle auquel l'orange a été découpé:

ou revenir à notre nomenclature précédente:

Pour calculer la latitude sur le cours du grand cercle, nous utilisons à nouveau le même ensemble:

comme nous aimons à utiliser une valeur de longitude spécifique pour p (au lieu de longitud navigué) nous devons ajuster la position de l'orange découpée aux coordonnées méridiens. Nous le faisons à travers l'intersection H:

Ainsi, nous obtenons notre équation pour la latitude du cours du grand cercle en fonction de la longitude:
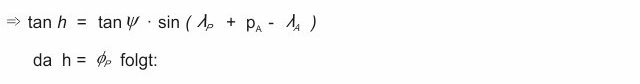


image 1
Le problème:nous voulons naviguer de A à B, les coordonnées (longitude et latitude) de départ et de destination sont connus, ce que nous voulons savoir:
- la distance
- Le cours sûr boussole nous devons suivre
La distance peut être calculée par la relation suivante, tirée de sources pertinentes (Wikipedia)


Si nous convertissons maintenant le résultat de degrés à arcminutes (multiplié par 60), on obtient la distance entre A et B en miles nautiques (une minute d'arc sur un grand cercle correspond par définition à un mile nautique).
Jusqu'ici tout va bien. Maintenant, le cours. La navigation classique propose la méthode du "triangle de navigation" qui est un triangle sphérique rectangle, nommé "pôle-triangle" et forme un angle droit au sommet (S) entre le cours du grand cercle et la distance au pôle Nord (ou Pôle Sud):

image 2
Avec outre sphérique trigonométrie vous obtenez le cours au départ et le course avec lequel vous arrivez à la destination, ainsi que les point de référence qui sont nécessaires pour les corrections de trajectoire à suivre le grand cercle et donc à la voile la plus courte distance.Après avoir été un temps occupé avec cela, je me souvins d'une méthode plus simple de comprendre pour moi. Comme un vieux penseur intransigeant, je préfère me orienter vers l'équateur plutôt qu'au pôle Nord (peut-être simplement parce qu'il est plus chaud là...) J'utilise ici le fait que chaque grand cercle recoupe exactement deux fois avec l'autre grand cercle sur le même monde, à savoir à 2 points exactement opposés de la sphère (appelons-les H). Il en va également de l'équateur avec notre cours grand cercle, comme suit:

image 3
M devrait être présente au centre de la terrePour le rendre un peu plus facile pour l'oeil humain, je coupe notre orange, coupé exactement sur la partie où l'équateur croise notre cours du grand cercle, le résultat est le suivant:

image 4
maintenant, nous voulons déterminer, pour toute longueur p (= longitudes naviguaient) la latitude associée pour obtenir des point de référence (P) sur notre cours - pour répondre à un grand cercle. Pour ce faire, nous devons d'abord trouver la position et l'angle du couper d'orange. Pour cela, nous utilisons l'équation suivante: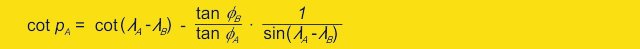
Je vais éviter d'expliquer la dérivation de cette équation pour le moment, les personnes intéressées peuvent trouver ci-dessous sur cette page.
pA nous dit les longitudes à passer pour avoir le baptême équatorial, ou parlé comme une fruiterie, au sommet de notre couper d'orange.
Et avec l'équation suivante, on obtient l'angle du couper d'orange:

(Dérivation pour les personnes intéressées à nouveau ci-dessous.)
Et maintenant, ce que nous voulions vraiment, une équation avec laquelle on peut déterminer la latitude correspondante sur le grand cercle pour toute longitud donnée:

(Dérivation comme toujours ci-dessous)
On pourrait encore continuer avec cela, par exemple, il serait très intéressant pour chaque point de référence, savoir le cours nous devrions naviguer (changer le cours sûr boussole), ou vous pourriez déterminer la longitude en fonction de la latitude, ou même une formule pour le cours en fonction de la distance déjà navigué. Avec les bases déjà développées, on peut tirer tout cela relativement rapidement avec trigonométrie sphérique, mais oui, je ne vais pas exagérer ici...
Ce que nous avons laissé est un
exemple de calcul:
Nous venons du Cap Horn, et nous tenons à traverser le Pacifique pour arriver sur les îles Fiji. Bien sûr, nous ne le ferions pas normalement, mais comme un exemple de calcul il fonctionne agréable :-)
Cap Horn:
55 degrés 59 min S = -55,98 degrés
67 degrés 17 min W = -67,28 degrees
îles Fiji:
18 degrés 8 min S = -18,13 degrés
178 degrés 26 min O = 178,43 degrés
Tout d'abord, nous déterminons la distance que nous devons naviguer:


= -0,8288 x -0,3112 + 0,5595 x 0,9504 x -0,4114
= -0,0400
arc cos -0,0400 = 87,71 degrees (x 60)
= 5.262 miles nautiques
Maintenant, nous définissons le pA nécessaire:
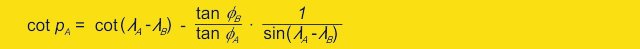
= -0,4513 - 0,2210 x 1,0971
= -0,6938
pA = -55,25 degrés
ainsi que l'angle du couper d'orange:

= -0,6750 x -0,8216
= 0,5545
l'angle du couper est donc 61 degrés.
pA est négatif: c'est seulement à cause que on n'a pas atteint le sommet de notre grand cercle lors de notre voyage, de sorte que cette valeur est réfléchie à l'intersection derrière nous (H' à la place de H), respectivement l'angle.
Maintenant, nous voulons déterminer cinq endroits sur le grand cercle, chacun au début et à la fin, et trois entre les deux. Notre formule:

Nos longitudes préétablies sont: -67,28 degrés (Cap Horn, début); 178,43 degrés (îles Fiji, fin); ainsi que -95 degrés; -125 degrés; -150 degrés. Donc, nous calculons aussi le départ et la destination, bien que les latitudes sont déjà connues, juste pour vérifier l'exactitude du calcul.
= 1,8034 x -0,8216 = -1,4817 -> latitude = -55,98 degrés, ok pour Cap Horn
= 1,8034 x -0,1815 = -0,3274 -> latitude = -18,13 degrés, ok pour îles Fiji
et les 3 points de référence:
= 1,8034 x -0,9925 = -1,7899 -> latitude = -60,81 degrés
= 1,8034 x -0,9207 = -1,6604 -> latitude = -58,94 degrés
= 1,8034 x -0,6695 = -1,2074 -> latitude = -50,36 degrés
Notre cours du grand cercle nous emmène donc du Cap Horn au départ vers le sud à 61 degrés de latitude (= l'angle du couper d'orange), probablement nous devons nous battre dur avec de la glace là avant, que nous nous dirigerons vers le nord et il va se réchauffer vers l'équateur...
John Franklin, Amerigo Vespucci et Sir Francis Drake vous saluer, que vous n'oubliez pas votre sextant sur le voyage s'il vous plaît, parce qu'ils étaient tous de grands mathématiciens et étaient voile encore sans GPS...
"Il y a quelque chose plus important que la logique: l'Imagination", Alfred Hitchcock
Derivations:
Nous considérons le triangle sphérique entre l'équateur, notre cours de grand cercle, et un point arbitraire P (voir l'image 5 ci-dessous). Ce triangle a d'excellentes propriétés, il est en fait un triangle sphérique à angle droit et permet donc des calculs facilement. Nous sommes intéressés par l'emplacement exact du couper d'orange, où notre parcours traverse l'équateur, et l'angle sous lequel on coupe l'orange. Connu sont 2 places P, le départ et la destination, chacune avec la latitude et la longitude. Dans ce triangle, nous utilisons un théorème de trigonométrie sphérique:

maintenant nous remplaçons hA, hB et Dp avec notre nomenclature précédente:
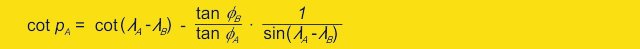
à partir de l'équation initiale, on obtient aussi l'angle auquel l'orange a été découpé:

ou revenir à notre nomenclature précédente:

Pour calculer la latitude sur le cours du grand cercle, nous utilisons à nouveau le même ensemble:

comme nous aimons à utiliser une valeur de longitude spécifique pour p (au lieu de longitud navigué) nous devons ajuster la position de l'orange découpée aux coordonnées méridiens. Nous le faisons à travers l'intersection H:

Ainsi, nous obtenons notre équation pour la latitude du cours du grand cercle en fonction de la longitude:
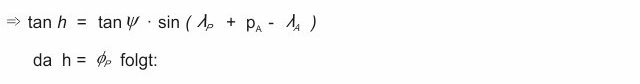

0 commentaires | laisser un commentaire
plus de photos de "Navigation orthodromique du grande cercle sur une orange":
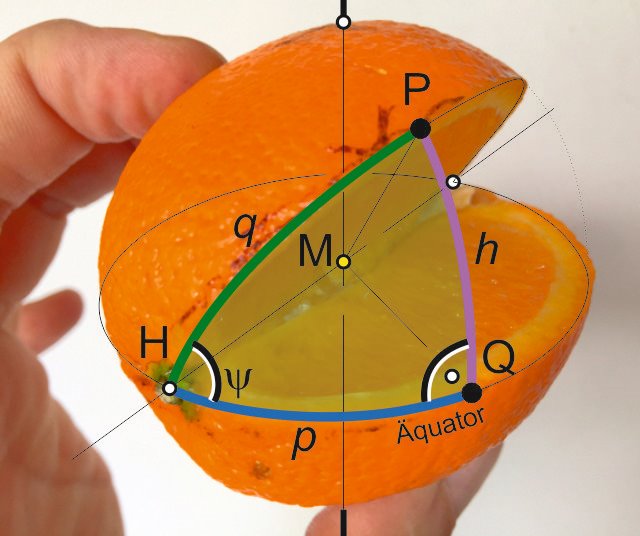
image 5

régate en Croatie

et les gagnants sont...

catégories: Sport
mots clés: Navigation, orthodromique, grande, cercle, une, orange
posté: 21.04.2016
vidéos
appartements
location de voiture
derniers posts:
Nouveaux appartements Las Piteras Patio
Il y a 25 ans
Les dernières conditions pour voyager à Espagne
Soyez prudent lors de la réservation des vols
Rabais d´été à Las Piteras
Joyeuses fêtes de Pâques
Las Piteras à Charco del Palo
L´exigence de masque à l´extérieur n´est plus applicable
Il y a 25 ans
Les dernières conditions pour voyager à Espagne
Soyez prudent lors de la réservation des vols
Rabais d´été à Las Piteras
Joyeuses fêtes de Pâques
Las Piteras à Charco del Palo
L´exigence de masque à l´extérieur n´est plus applicable
Encore une fois
Bonne année 2022
Masque à nouveau obligatoire en Espagne à partir du réveillon de Noël
Noël 2021
Réservez votre voiture de location dès que possible
Éruption du volcan Cumbre Vieja à La Palma
Enfin sans masque
Bonne année 2022
Masque à nouveau obligatoire en Espagne à partir du réveillon de Noël
Noël 2021
Réservez votre voiture de location dès que possible
Éruption du volcan Cumbre Vieja à La Palma
Enfin sans masque
Catégories:
AppartementsCharco del Palo
Site Internet
Plage
Excursions
Animaux
Météo
Natation
Événements
Restaurants
Musicaux
Sport
Voile
Corona virus




